
[Prepwork 3.5]
Q1. The Bay of Monterey in California is known for extreme tides. The depth of the water, y, in meters can be modeled as a function of time, t, in half-hours after midnight, by y=12+6cos(t). How quickly is the depth of the water rising or falling at 3 a.m.? (Make sure you compute this in radians and give your answers to three decimal places.)
Rising at (in m/half-hours)
A: 1.676
Q2. For how many values of its domain is the derivative of the cosine function equal to zero?
A: Infinitely many values
[HW 3.5]
Q1. Find the derivative of 𝑠(𝑞)=18 cos𝑞 sin𝑞
A: s'(q) = 18(cos^2(q)-sin^2(q)

Q2. Find the derivative of R(x) = 16 - 6cos(𝜋𝑥)
A: R'(x) = 6𝜋sin(𝜋𝑥)

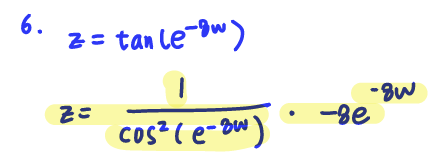
Q3. Find the derivative of f(x) = x^6*cos(x)
A: f'(x) = 6x^5*cos(x) - sin(x)*x^6
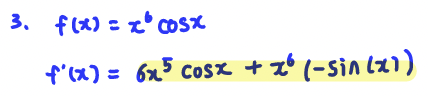
Q4. Find the derivative of f(x) = 4.15^(cos(x))
A: f'(x) = (ln (4.15)(4.15^(cos(x))(-sin(x))
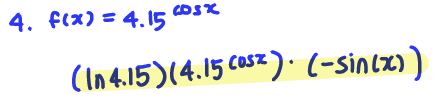
Q5. Find the derivative of f(x) = (1-sin(x))^(1/7)
A: f'(x) = (1/7)(1-sin(x))^(-6/7)*(-cos(x))
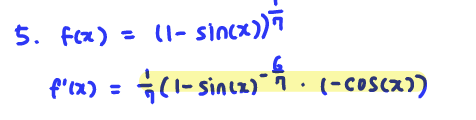
Q6. Find the derivative of z = tan(e^(-8w))
A: dz/dw = (1/(cos^2*(e^(-8w))*(-8e^(-8w))
Q7. Find the derivative of y = cos^2(w) + cos(w^2)
A: dy/dw = 2*cos(w)*(-sin(w))+(-sin(w^2))*2w
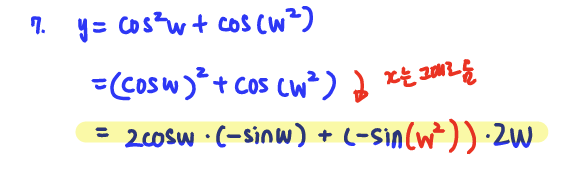
Q8. A boat at anchor is bobbing up and down in the sea. The vertical distance, y, in feet, between the sea floor and the boat is given as a function of time, t, in minutes, by y=29+cos(2πt) ft.
Find the vertical velocity, v, of the boat at time t.
A: v = -sin(2πt)*2π ft/min

'[Umich] COE Core > MATH 115 (Calc 1)' 카테고리의 다른 글
| [Notes & HW Answers] 3.7 Implicit Functions (0) | 2022.11.21 |
|---|---|
| [Notes & HW Answers] 3.6 The Chain Rule and Inverse Functions (0) | 2022.11.21 |
| [Notes & HW Answers] 3.4 The Chain Rule (0) | 2022.11.21 |
| [Notes & HW Answers] 3.3 The Product and Quotient Rules (0) | 2022.10.30 |
| [Notes & HW Answers] 3.2 The Exponential Functions (0) | 2022.10.28 |




댓글