[Notes & HW Answers] 3.6 The Chain Rule and Inverse Functions

[Notes & HW Answers] 3.6 The Chain Rule and Inverse Functions.pdf

1.10MB

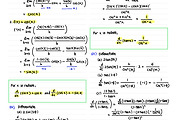
[Prepwork 3.6]

Q1. Let 𝑔(𝑥)g(x) be an invertible, differentiable function with values given in the table below.

𝑥	2	5	8
𝑔(𝑥)	8	2	0
𝑔′(𝑥)	-2	-0.25	-0.1

Find a formula for the tangent line of 𝑔^(−1)(𝑥) at 𝑥=2.

A: y = -4(x-2)+5

Q2. Find the derivative of 𝑓(𝑥)=arctan(5ln(𝑥)).

A: f'(x) = 5/(x*(25*ln^2(x)+1)

[HW 3.6]

Q1. Find the derivative of the function f(t), below. 

f(t) = ln(t^9 +8)

A: f'(t) = 9t^8/(t^9+8)

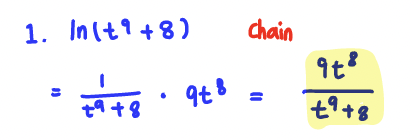
Q2. Find the derivative of the function j(x), below. Assume that n and p are constants. 

A: j'(t) = ne^(nx) / (e^(nx) + p)

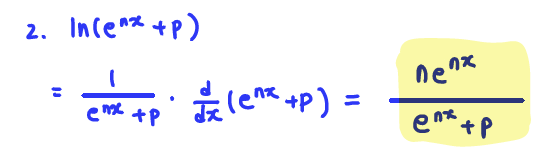
Q3. Find the derivative of the function f(y), below. It may be to your advantage to simplify before differentiating.

f(y) = arcsin(y^2) 

A: f'(y) = 2y/(1-y^4)^(1/2)

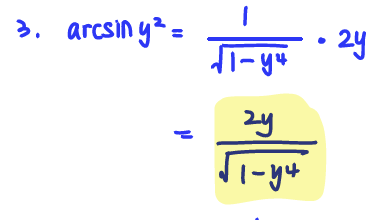
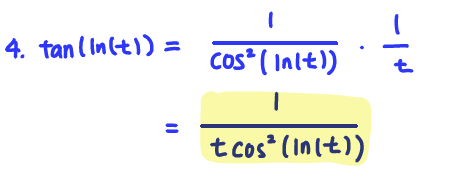
Q4. Find the derivative of the function g(t), below. It may be to your advantage to simplify before differentiating.

g(t) = tan(ln(t))

A: g'(t) = 1/(cos^2(ln(t))*t

Q5. Find the derivative of the function h(w), below. It may be to your advantage to simplify before differentiating.

h(w) = 8w*arcsin(w) 

A: h'(w) = 8*arcsin(w) + 8w* (1/(1-w^2))

Q6. Find the derivative of the function f(t), below.

f(t) = ln(ln(4t)) + ln(ln7)

A: f'(t) = 1/t*ln(4t)