

[Prepwork 3.9]
Q1. What is the value at x=.1 of the local linearization L(x) of (1+x)^5 at x=0?
A: L(0.1) = 1.5
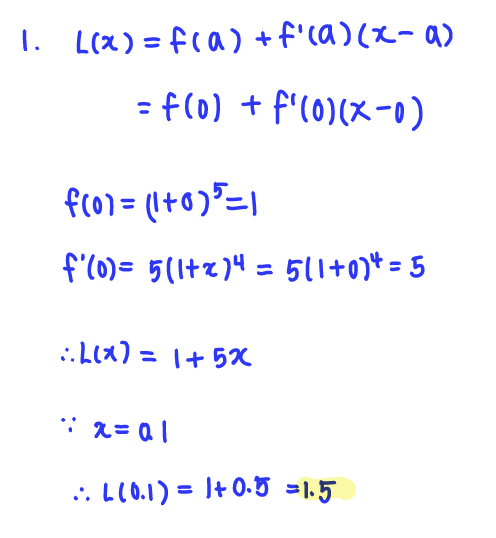
Q2. Suppose you use the tangent line approximation near t=4 to estimate s′(4.05), where s(t) is a function that is always concave up. Then your answer is an
A: underestimate
Q3. Suppose the linear approximation of g(x)g(x) near x=6 is given by L(x)=5(x−6)−12.
A:Then g(6) = -12 and g'(6) = 5.
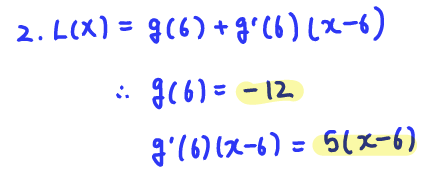
[HW 3.9]
Q1. Find the tangent line approximation for (4+x)^(1/2) near x = 0.
A: y= 2+ (1/4)x
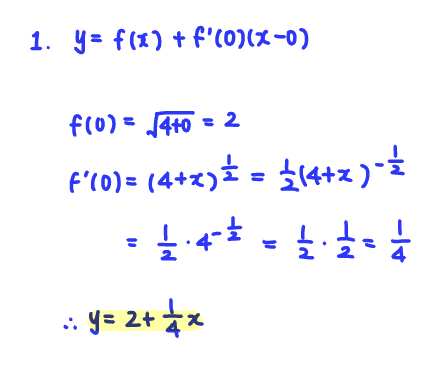
Q2. Near x=0, the tangent line approximation gives 2e−5x≈
A: 2-10x
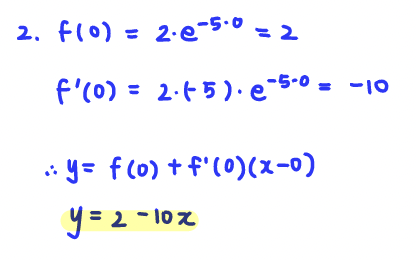
Q3. Suppose f′(x) is a differentiable increasing function for all x. In each of the following pairs, which number is the larger?
For each, enter A or B.
A: 1. Comparing A. f'(9) and B. f'(10): B is larger.
2. Comparing A. f''(9) and B.0: A is larger.
3. Comparing A. f(9+Δx) and B. f(9) + f'(9)Δx: A is larger.
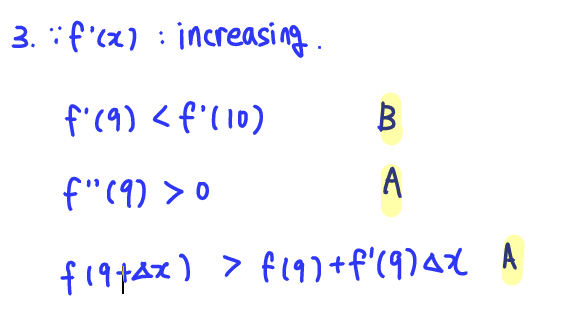
'[Umich] COE Core > MATH 115 (Calc 1)' 카테고리의 다른 글
| [Notes & HW Answers] 4.1 Using First and Second Derivatives (0) | 2022.12.06 |
|---|---|
| [Notes] 3.10 Theorems About Differentiable Functions (0) | 2022.11.29 |
| [Notes & HW Answers] 3.7 Implicit Functions (0) | 2022.11.21 |
| [Notes & HW Answers] 3.6 The Chain Rule and Inverse Functions (0) | 2022.11.21 |
| [Notes & HW Answers] 3.5 The Trigonometric Functions (0) | 2022.11.21 |




댓글