

[Prepwork 3.4]
Q1. The length,L, in micrometers (𝜇μm), of steel depends on the air temperature degrees celsius, and the temperature depends on time,t, measured in hours. If the length of a steel bridge increases by 0.25μm for every degree increase in temperature, and the temperature is increasing at 4 degrees celsius per hour, how fast is the length of the bridge increasing?
A: At a rate of 1 μm/hour
Q2. How many times would we need to use the chain rule to differentiate 𝑓(𝑥)=(1+e^((3+x^2)^1/2))^1/2
A: 3

[HW 3.4]
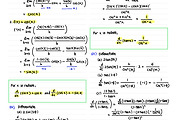
Q1. Find the derivative of w = (t^3 + 2)^67
A: dw/dt = 201(t^3+2)^66*t^2

Q2. Find the derivative of 𝑓(𝑥)= e^(7x)*(x^2+4^x)
A: f'(x) = 7e^(7x)*(x^2+4^x) + e^(7x)*(2x + (ln 4)4^x)

Q3. Find the derivative of v(t) = t^5*e^(-ct). Assume that c is a constant.
A: v'(t) = e^(-ct)*(5*t^4-c*t^5)

Q4. Find the derivative of f(x) = (ax^2 + b)^5. Assume that a and b are constants.
A: f'(x) = 5(ax^2+b)^4*(2ax)
Q5. Find the derivative of h(z) = (b/(a+z^2)^3. Assume that a and b are constants.
A: h'(z) = 3(b/(a+z^2)^2*(-2bz)/(z^2+a)^2

Q6. Find the derivative of y = (e^(-6t^2) +8)^(1/2).
A: dy/dt = (1/2)(e^(-6t^2)+8)^(-1/2)*(-12t*e^(-6t^2))

Q7. Use the graph below to find exact values of the indicated derivatives, or state that they do not exist. If a derivative does not exist, enter dne in the answer blank. The graph of 𝑓(𝑥)f(x) is black and has a sharp corner at 𝑥=2x=2. The graph of 𝑔(𝑥)g(x) is blue.

Let h(x) = f(g(x)). Find
A: (A) h'(1) = -3/8
(B) h'(2) = -3/8
(C) h'(3) = -3/8
Q8. For what values of 𝑥 is the graph of 𝑦=𝑥𝑒^(−4𝑥) concave down?
A: values = (−∞,1/2)
(Give your answer as an interval or a list of intervals, e.g., (-infinity,8] or (1,5),(7,10) .


'[Umich] COE Core > MATH 115 (Calc 1)' 카테고리의 다른 글
| [Notes & HW Answers] 3.6 The Chain Rule and Inverse Functions (0) | 2022.11.21 |
|---|---|
| [Notes & HW Answers] 3.5 The Trigonometric Functions (0) | 2022.11.21 |
| [Notes & HW Answers] 3.3 The Product and Quotient Rules (0) | 2022.10.30 |
| [Notes & HW Answers] 3.2 The Exponential Functions (0) | 2022.10.28 |
| [Notes & HW Answers] 3.1 Powers and Polynomials (0) | 2022.10.28 |



댓글