[Notes & HW Answers] 3.2 The Exponential Functions

[Notes & HW Answers] 3.2 The Exponential Functions.pdf

0.97MB

[Prepwork 3.2]

Q1. Let f (x) = x^10 +10^x. Find the first and second derivatives of f(x).

A: f'(x) = 10x^9 + (ln 10)10^x ; f''(x) = 90x^8+(ln 10)(ln10)10^x

 

Q2. For what value of a is y = 1+5x the tangent line for y = ax at x = 0?

A: a = e^5 

 

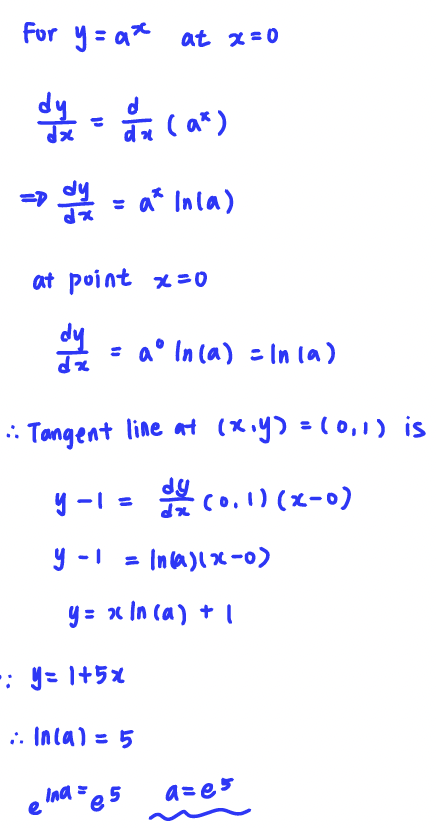
[HW 3.2]

Q1. Find the derivative of y = 4x^8+8^x+12.

A: dy/dx = 32x^7 + (ln 8)8^x

Q2. Find the derivative of z = (ln 10)e^x.

A: dz/dx = (ln 10)e^x. 

Q3. Find the derivative of f(t) = (ln7)t

A: f'(t) = ln(ln 7)*ln7^t

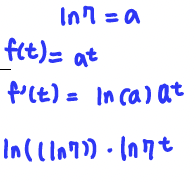
Q4. Find the derivative of f(x) = e^n +n^x. Assume that n is a positive constant.

A: f'(x) = ln(n)n^x

Q5. Find the derivative of f(t) = e^(t+2)

A: e^(t+2) 

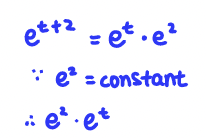
Q6. Certain pieces of antique furniture increased very rapidly in price in the 1970s and 1980s. For example, the value of a particular rocking chair is well approximated by V = 90(1.75)t , where V is in dollars and t is the number of years since 1975. Find the rate, in dollars per year, at which the price is increasing.

A: rate = 90(ln 1.75)1.75t dollars/yr