
[Prepwork 4.5]
Q1. What is the relationship between (total) cost and marginal cost?
A: Marginal cost is the derivative of total cost
Q2. Suppose C and R are the cost and revenue functions for a particular product.
Check all the statements below that are true.
A. The critical points of the profit function happen when 𝑀𝑅=𝑀𝐶 or one of these derivatives does not exist.
B. The profit is maximized when the difference between 𝑀𝑅MR and 𝑀𝐶MC is greatest.
C. Any time 𝑀𝑅=𝑀𝐶MR=MC, the profit is maximized.
Q3. Find the quantity 𝑞 that maximizes profit if the total revenue, 𝑅(𝑞), and total cost, 𝐶(𝑞) are given in dollars by 𝑅(𝑞)=5𝑞−0.002𝑞^2 and 𝐶(𝑞)=200+2.2𝑞, where 0≤𝑞≤2500 units.
A: q = 700
? They refer to the same thing Marginal cost is the minimal possible cost There is no simple relationship between the two Total cost is the derivative of marginal cost
y = f (x) such that f'(x) = 10x^9*e^x+x^10*e^x?
• A. x10ex+10
[HW 4.5]
Q1. The figure below shows cost (blue) and revenue (black) functions over the domain 0<𝑞<45 (in thousands of units).
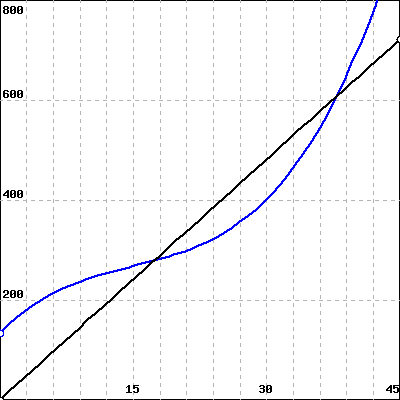
A: For what production levels is the profit function positive? (18,38)
(Give your answer as an interval or a list of intervals, e.g., (-infinity,8] or (1,5),(7,10) .)
For what production levels is the profit function negative? (0,18),(38,45)
(Give your answer as an interval or a list of intervals, e.g., (-infinity,8] or (1,5),(7,10) .)
Estimate the production at which profit is maximized. 𝑞≈ 30 thousands of units.
Q2. The revenue from selling 𝑞 items is 𝑅(𝑞)=500𝑞−𝑞^2, and the total cost is 𝐶(𝑞)=100+14𝑞. Write a function that gives the total profit earned, and find the quantity which maximizes the profit.
A: Profit 𝜋(𝑞)= 500q−q^2−100−14q
Quantity maximizing profit 𝑞= 243
Q3. The table below shows cost, 𝐶(𝑞), and revenue, 𝑅(𝑞).
| 𝑞 | 0 | 500 | 1000 | 1500 | 2000 | 2500 | 3000 |
| 𝑅(𝑞) | 0 | 1875 | 3750 | 5625 | 7500 | 9375 | 11250 |
| 𝐶(𝑞) | 2750 | 4077.5 | 4741.25 | 5257.5 | 5773.75 | 6953.75 | 10125 |
A: At approximately what production level, 𝑞, is profit maximized?
𝑞≈ 2500 units
What is the price of the product?
price = 3.75 dollars
What are the fixed costs?
fixed costs = 2750 dollars
Q4. The average cost per item to produce 𝑞 items is given by
What is the total cost, 𝐶(𝑞), of producing 𝑞 goods?
𝐶(𝑞)= q(0.01q^2−1.2q+43)
What is the minimum marginal cost?
minimum MC = −5
At what production level is the average cost a minimum?
𝑞= 60
What is the lowest average cost?
minimum average cost = 7
Compute the marginal cost at 𝑞=60.
𝑀𝐶(60)= 7
'[Umich] COE Core > MATH 115 (Calc 1)' 카테고리의 다른 글
| [Notes & HW Answers] 5.1 How Do We Measure Distance Traveled? (0) | 2022.12.06 |
|---|---|
| [Notes & HW Answers] 4.6 Related Rates (0) | 2022.12.06 |
| [Notes & HW Answers] 4.4 Families of Functions and Modeling (0) | 2022.12.06 |
| [Notes & HW Answers] 4.3 Optimization and Modeling (0) | 2022.12.06 |
| [Notes & HW Answers] 4.2 Optimization (0) | 2022.12.06 |




댓글