
[Prepwork 4.3]
Q1. Consider the following problem:
You are standing on a river bank and want to get to a house that is on the other side of the river and 800 feet up the river as quickly as possible. The river is 100 feet wide. You can walk along the river at a speed of 5 ft/sec or swim across the river at a speed of 3 ft/sec. What path should you take?
A:
Which of the following quantities are you trying to optimize? The time it takes you to get to the house
Are you trying to minimize or maximize this quantity? Minimize
Q2. Follow the work in example 1 in this section of the textbook to find an equation (in terms of the radius 𝑟) for the total material used in a can having a volume of 90 cubic inches.
A:
M(r) = 2pi*r^2+180/r

Q3. Use the work in example 4 in this section of the textbook to find a formula for the volume of a box having surface area 5.
A:
V(x) = (x/4)*(5-2x^2)
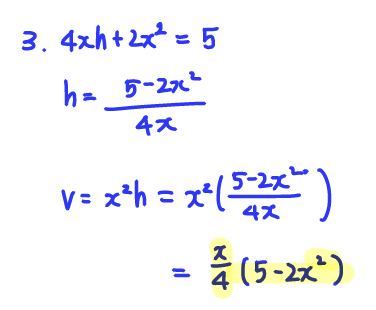
[HW 4.3]
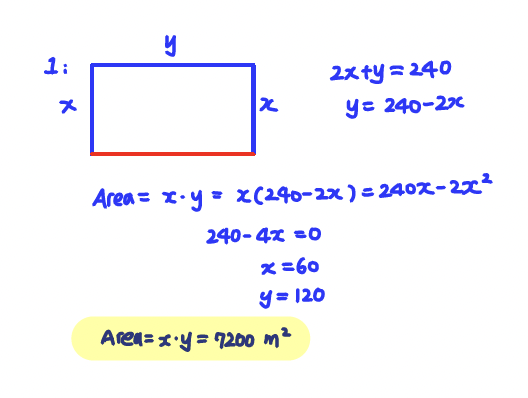
Q1. If you have 240 meters of fencing and want to enclose a rectangular area up against a long, straight wall, what is the largest area you can enclose?
A: Area = 7200 m^2
Q2. A rectangle has one side on the 𝑥x-axis and two vertices on the curve
Find the vertices of the rectangle with maximum area.
A: Vertices = (−√3,0),(√3,0),(−√3,13),(√3,13)
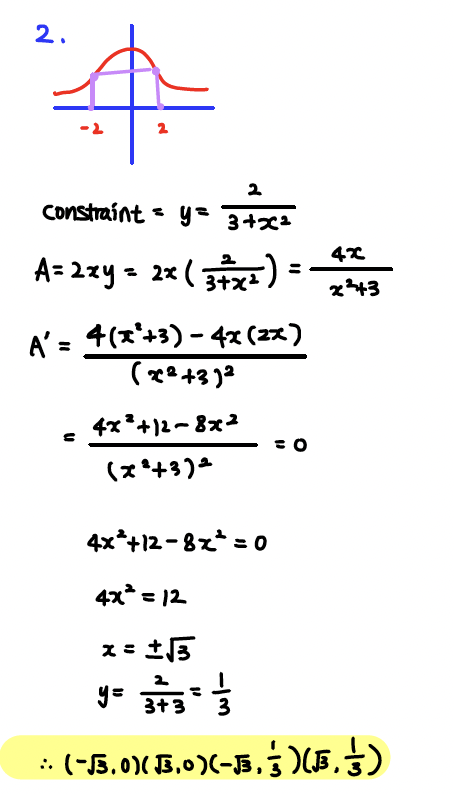
Enter your answers as a comma-separated list of ordered (x,y) pairs, e.g., (1,0),(8,0),(1,4),(8,4).
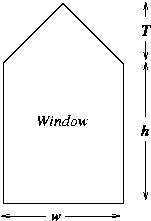
Q3. Consider a window the shape of which is a rectangle of height ℎh surmounted by a triangle having a height 𝑇 that is 0.7 times the width 𝑤 of the rectangle (as shown in the figure below).
A:
If the cross-sectional area is 𝐴, determine the dimensions of the window which minimize the perimeter.
ℎ= (A−0.35((2A/(2·0.74((1/2)+0.3)))/((2A/2·0.74^(1/2)+0.3))^(1/2)
𝑤= ((2A/(2·0.74^(1/2)+0.3))^(1/2)

Q4. A hemisphere of radius 1 sits on a horizontal plane. A cylinder stands with its axis vertical, the center of its base at the center of the sphere, and its top circular rim touching the hemisphere. Find the radius and height of the cylinder of maximum volume.
A:
radius = (2/3)^(1/2)
height = (1/3)^(1/2)
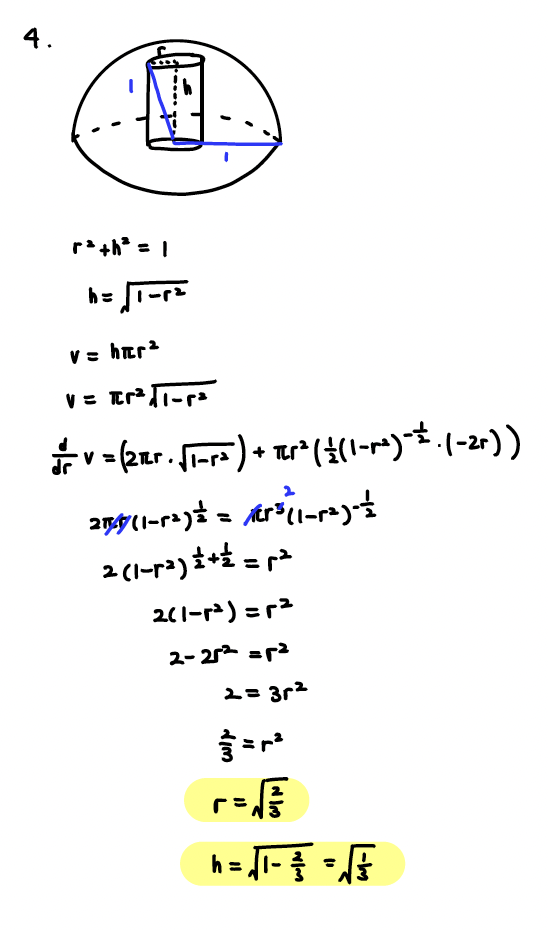
'[Umich] COE Core > MATH 115 (Calc 1)' 카테고리의 다른 글
| [Notes & HW Answers] 4.5 Applications to Marginality (0) | 2022.12.06 |
|---|---|
| [Notes & HW Answers] 4.4 Families of Functions and Modeling (0) | 2022.12.06 |
| [Notes & HW Answers] 4.2 Optimization (0) | 2022.12.06 |
| [Notes & HW Answers] 4.1 Using First and Second Derivatives (0) | 2022.12.06 |
| [Notes] 3.10 Theorems About Differentiable Functions (0) | 2022.11.29 |




댓글