

[Prepwork 4.2]
Q1. Which of the following examples satisfy the hypotheses of the Extreme Value Theorem on the given interval?
(A) k(x)={3x^2+9 for 0≤x<2; 12x for 2≤x≤ 10 on 0≤x≤10
(B) g(x)=6x^2+3 on 0≤x≤4
(C) f(x)=1/x on −10≤x≤10
(D) m(x)=6x^3+x+1 on −4<x≤20
(E) h(x)=e^x/x on 2≤x≤16
Answer: B,E
Q2. Let f(x)=2x^3−12x^2+18x+16. Find the minimal value of f(x) on the interval −1≤x≤2.
Answer: The minimum value of f(x) on this interval is −16 and occurs at x=−1.
Q3. Suppose f(x)f(x) is a continuous function defined on −∞<x<∞−∞<x<∞ with exactly two critical points. Which of the following statements are true?Check all that are true.
A:
(A) f(x) may or may not have global extrema
(B) f(x) may have a global maximum at more than one xx-value
(C) f(x) may have a global minimum or a global maximum, but cannot have both
(D) f(x) cannot have any global extrema
(E) f(x) must have both a global maximum and a global minimum
[HW 4.2]
Q1. Find the exact global maximum and minimum values of the function 𝑔(𝑡)=6𝑡𝑒^(−5𝑡) if 𝑡>0.
A:
global maximum at 𝑡= 1/5
global minimum at 𝑡= none
(Enter none if there is no global maximum or global minimum for this function.)
Q2. Find the exact global maximum and minimum values of the function 𝑓(𝑡)=3𝑡/(8+𝑡^2) if its domain is all real numbers.
A:
global maximum at 𝑡= 8^(1/2)
global minimum at 𝑡= -8^(1/2)
(Enter none if there is no global maximum or global minimum for this function.)
Q3. For some positive constant 𝐶, a patient's temperature change, 𝑇, due to a dose, 𝐷, of a drug is given by 𝑇=(𝐶/2−𝐷/3)*𝐷^2.
A:
What dosage maximizes the temperature change?
𝐷= C
The sensitivity of the body to the drug is defined as 𝑑𝑇/𝑑𝐷. What dosage maximizes sensitivity?
𝐷= C/2
Q4. When an electric current passes through two resistors with resistance 𝑟 and 𝑠, connected in parallel, the combined resistance, 𝑅, can be calculated from the equation
where 𝑅, 𝑟, and 𝑠 are positive. Assume that 𝑠 is constant.
A:
Find 𝑑𝑅/𝑑𝑟:
𝑑𝑅/𝑑𝑟= 𝑅^2/𝑟^2
Is 𝑅 and increasing or decreasing function of 𝑟? increasing
(Enter increasing, decreasing, neither, or both (write both if there are values of 𝑟r for which 𝑅R is increasing, and other values for which it is decreasing; enter neither if this is a constant function.)
If we consider the interval 𝑎≤𝑟≤𝑏, where does 𝑅 take on its global maximum and minimum values?
maximum: 𝑟=b
minimum: 𝑟=a
(Enter none if there is no global maximum or minimum for this function.)
Q5. The figure below gives the behavior of the derivative of 𝑔(𝑥) on −2≤𝑥≤2.
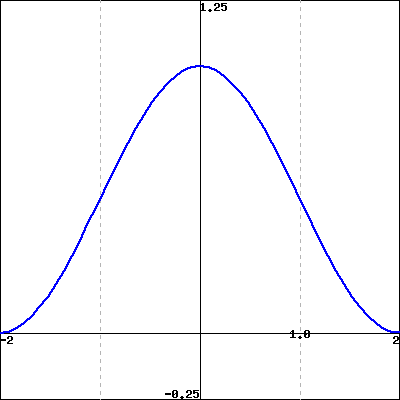
Graph of 𝑔′(𝑥) (not 𝑔(𝑥))
Sketch a graph of 𝑔(𝑥)g(x) and use your sketch to answer the following questions.
A. Where does the graph of 𝑔(𝑥) have inflection points?
𝑥= 0
Enter your answer as a comma-separated list of values, or enter none if there are none.
B. Where are the global maxima and minima of 𝑔g on [−2,2]?
minimum at 𝑥= −2
maximum at 𝑥= 2
C. If 𝑔(−2)=1, what are possible values for 𝑔(0)?
𝑔(0) is in (1,3]
(Enter your answer as an interval, or union of intervals, giving the possible values. Thus if you know 5<𝑔(0)≤8, enter (5,8]. Enter infinity for ∞, the interval [-4,-4] to indicate a single point).
How is the value of 𝑔(2) related to the value of 𝑔(0)?
𝑔(2) > 𝑔(0)
(Enter the appropriate mathematical equality or inequality, =, <, >, etc.)
Q6. A smokestack deposits soot on the ground with a concentration inversely proportional to the square of the distance from the stack. With two smokestacks 𝑑 miles apart, the concentration of the combined deposits on the line joining them, at a distance 𝑥 from one stack, is given by
where 𝑐 and 𝑘 are positive constants which depend on the quantity of smoke each stack is emitting. If 𝑘=5𝑐, find the point on the line joining the stacks where the concentration of the deposit is a minimum.
A:
𝑥min = d/5^(1/3)+1 mi
'[Umich] COE Core > MATH 115 (Calc 1)' 카테고리의 다른 글
| [Notes & HW Answers] 4.4 Families of Functions and Modeling (0) | 2022.12.06 |
|---|---|
| [Notes & HW Answers] 4.3 Optimization and Modeling (0) | 2022.12.06 |
| [Notes & HW Answers] 4.1 Using First and Second Derivatives (0) | 2022.12.06 |
| [Notes] 3.10 Theorems About Differentiable Functions (0) | 2022.11.29 |
| [Notes & HW Answers] 3.9 Linear Approximation (0) | 2022.11.21 |




댓글