
[Prepwork 5.3]
Q1. Around the beginning of the 1800’s, the population of the U.S. was growing at a rate of about 1.37t million people per decade, with t being measured in decades from 1810.If the population P(t) was 7.2 million people in 1810, estimate the population in 1820 (one decade later) by considering the work in example 2.
A: P(1)= 8.375309
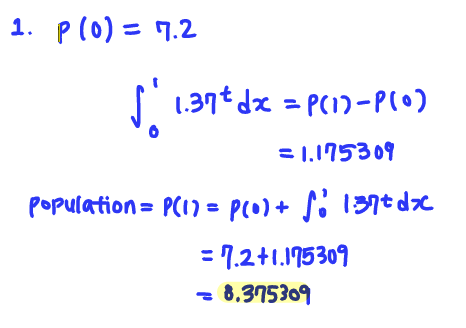
Q2. Given the CO2 addition rate shown in example 4 (note that values from the graph are given in a table at the end of the example), estimate the amount of CO2 that enters the pond between t=16 and t=20:

Q3. Use the Fundamental Theorem of Calculus to calculate:

[HW 5.3]
Q1. If V(x) is the rate of change of the volume of a live band in decibels/m and x is the distance from the stage in m, consider the integral
Be sure that you can explain in words the meaning of this integral.
What are the units of the integral?
A. decibels/m^2
B. decibels m/ s
C. decibels/m
D. decibels m
E. decibels/s
F. none of the above
Q2. For the function F(t)=e^t^2, let f(t)=F′(t). Write the integral ∫^b_a f(t) dt and evaluate it with the Fundamental Theorem of Calculus.
A: ∫^2_0 2t*e^t^2 dt = e^4−1

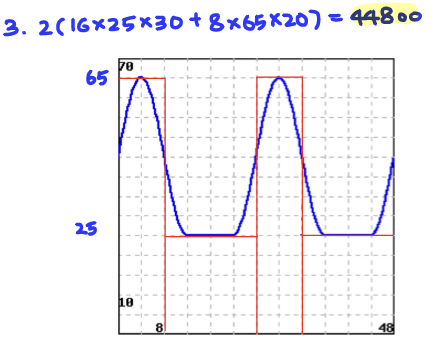
Q3. A two-day environmental clean up started at 9AM on the first day. The number of workers fluctuated as shown in the following figure.
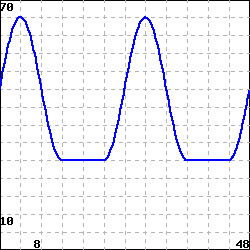
Suppose that the workers were paid 20 dollars per hour for work during the time period 9 am to 5 pm and were paid 30 dollars per hour for work during the rest of the day. What would the total personnel costs of the clean up have been under these conditions?
A: total cost = 44800 dollars
Q4. A student is speeding down Route 11 in his fancy red Porsche when his radar system warns him of an obstacle 400 feet ahead. He immediately applies the brakes, starts to slow down, and spots a skunk in the road directly ahead of him. The "black box" in the Porsche records the car's speed every two seconds, producing the following table. The speed decreases throughout the 10 seconds it takes to stop, although not necessarily at a uniform rate.
| Time since brakes applied (sec) | 0 | 2 | 4 | 6 | 8 | 10 |
| Speed (ft/sec) | 115 | 85 | 55 | 25 | 5 | 0 |
A. What is your best estimate of the total distance the student's car traveled before coming to rest (note that the best estimate is probably not the over or under estimate that you can most easily find)?
distance = 455 ft
B. Which one of the following statements can you justify from the information given?
(1) The "black box" data is inconclusive. The skunk may or may not have been hit.
(2) The car stopped before getting to the skunk.
(3) The skunk was hit by the car.

Q5. The following table gives the the approximate amount of emissions, E, of nitrogen oxides in millions of metric tons per year in the US. Let t be the number of years since 1940 and E=f(t).
| 1940 | 1950 | 1960 | 1970 | 1980 | 1990 | |
| t | 0 | 10 | 20 | 30 | 40 | 50 |
| E | 6.4 | 9.6 | 12.9 | 18.6 | 21.3 | 19.9 |
A: Estimate the integral: ∫^50_0 f(t) dt≈ 755.5

Q6. Coal gas is produced at a gasworks. Pollutants in the gas are removed by scrubbers, which become less and less efficient as time goes on. The following measurements, made at the start of each month, show the rate at which pollutants are escaping (in tons/month) in the gas:
| Time (months) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Rate | 3 | 6 | 10 | 17 | 26 | 38 | 51 |
A. Make an overestimate and an underestimate of the total quantity of pollutants that escape during the first month.
overestimate = 6 tons
underestimate = 3 tons
B. Make an overestimate and an underestimate of the total quantity of pollutants that escape for the whole six months for which we have data.
overestimate = 148
underestimate = 100
C. How often would measurements have to be made to find an overestimate and an underestimate (for the quantity of pollutants that escaped) during the first six months which differ by exactly 1 ton from each other?
48 times a month.

'[Umich] COE Core > MATH 115 (Calc 1)' 카테고리의 다른 글
| [Notes & HW Answers] 6.1 Antiderivatives Graphically and Numerically (0) | 2022.12.08 |
|---|---|
| [Notes & HW Answers] 5.4 Theorems about Definite Integral (0) | 2022.12.06 |
| [Notes & HW Answers] 5.2 The Definite Integral (0) | 2022.12.06 |
| [Notes & HW Answers] 5.1 How Do We Measure Distance Traveled? (0) | 2022.12.06 |
| [Notes & HW Answers] 4.6 Related Rates (0) | 2022.12.06 |




댓글