

[Prepwork 5.2]
Q1. Following example 1 in the text, suppose we considered n=4 to approximate the integral. What are each of the following?
Q2. Find the exact value of the following integral.
A: ∫^2_(-2) (4-x^2)^(1/2) dx = 2π
Estimate the total area between f(x)=cos(x4) and the x-axis for (0≤x≤π)^(1/4)(Note: you will want to sketch the curve y=f(x). Shade the regions between the curve and the axis. You want the actual area of all of the shaded regions. You will want to use a calculator or similar tool to get a sufficiently accurate estimate.)
A: Area = 1.106911
[HW 5.2]
Q1. Consider the following table:
| x | 0 | 4 | 8 | 12 | 16 | 20 |
| f(x) | 33 | 32 | 30 | 26 | 18 | 2 |
Use this to estimate the integral:
A: ∫^20_0 f(x)dx ≈ 494

Q2: The graph of a function f(t) is given below.

Which of the following numbers could be an estimate of ∫^1.5_0 f(x)dx accurate to two decimal places?
A. 75.015
B. 150.18
C. -150
D. 149.985
E. 153.525
F. 138.705
G. 107.76
H. -147.525

Q3: Use the following figure, which shows a graph of f(x) to find each of the indicated integrals.

Note that the first area (with vertical, red shading) is 55 and the second (with oblique, black shading) is 5.
A. ∫^b_a f(x) dx=−55
B. ∫^c_b f(x) dx= 5
C. ∫^c_a f(x) dx= −50
D. ∫^c_a |f(x)| dx= 60
Q4: Use the graph of f(x) shown below to find the following integrals.

A. ∫^0_−3 f(x) dx= −4
B. If the vertical red shaded area in the graph has area A, estimate: ∫^5_−3 f(x) dx= −A
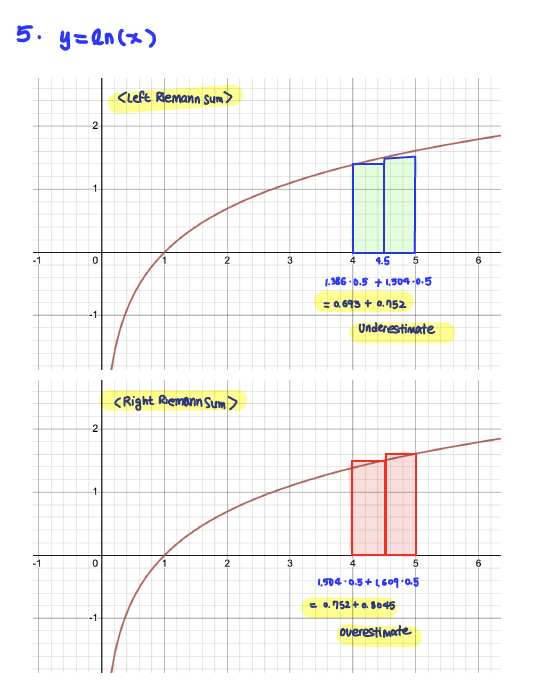
Q5: On a sketch of y=ln(x), represent the left Riemann sum with n=2 approximating ∫^5_4ln(x) dx. Write out the terms of the sum, but do not evaluate it:
Sum = 0.693 + 0.752
On another sketch, represent the right Riemann sum with n=2 approximating ∫^5_4 ln(x) dx. Write out the terms of the sum, but do not evaluate it:
Sum = 0.752 + 0.8045
Which sum is an overestimate?
A. the left Riemann sum
B. the right Riemann sum
C. neither sum
Which sum is an underestimate?
A. the left Riemann sum
B. the right Riemann sum
C. neither sum
'[Umich] COE Core > MATH 115 (Calc 1)' 카테고리의 다른 글
| [Notes & HW Answers] 5.4 Theorems about Definite Integral (0) | 2022.12.06 |
|---|---|
| [Notes & HW Answers] 5.3 The Fundamental Theorem of Calculus (0) | 2022.12.06 |
| [Notes & HW Answers] 5.1 How Do We Measure Distance Traveled? (0) | 2022.12.06 |
| [Notes & HW Answers] 4.6 Related Rates (0) | 2022.12.06 |
| [Notes & HW Answers] 4.5 Applications to Marginality (0) | 2022.12.06 |




댓글