[Notes & HW Answers] 5.1 How Do We Measure Distance Traveled?

[Notes & HW Answers] 5.1 How Do We Measure Distance Traveled.pdf

2.85MB

[Prepwork 5.1]

Q1. Consider the velocity data for the car shown in table 5.1. Find lower and upper estimates for the distance it travels between 𝑡=4 and 𝑡=8.

A:

lower = 164
upper = 184

Write the difference between these as the following product:

difference = (Δ𝑡)(Δ𝑣)= (2) (10)

Q2. The velocity of a bicycle is given by v(t) = 4t feet per second, where t is the number of seconds after the bike starts moving. How far does the bicycle travel in 3 seconds?

A: Distance = 18 ft

 

Q3. Suppose that the velocity of a ball is given, in meters/second, by the graph below.

Between 𝑡=0 and 𝑡=5:

What is the ball’s change in position? 7.5 m
What is the total distance that the ball traveled? 8.5 m

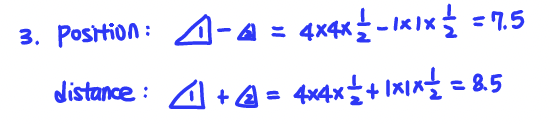
[HW 5.1]

Q1. The velocity 𝑣(𝑡) in the table below is increasing for 0≤𝑡≤12.

𝑡	0	3	6	9	12
𝑣(𝑡)	31	36	37	38	40

A. Find an upper estimate for the total distance traveled using
𝑛=4 subdivisions: distance traveled = 453
𝑛=2 subdivisions: distance traveled = 462

B. Which of the two answers in part (A) is more accurate?
𝑛= 4 is more accurate

C. Find a lower estimate for the total distance traveled using 𝑛=4.
distance traveled = 426

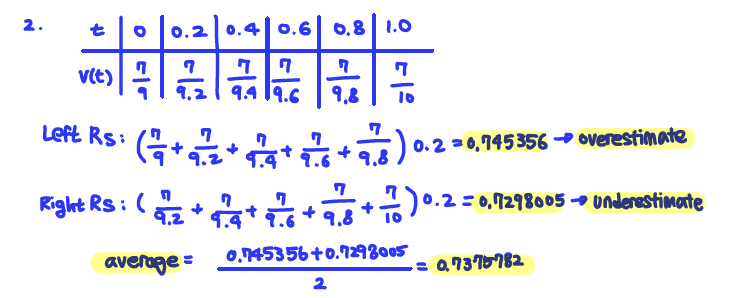
Q2. For time, 𝑡, in hours, 0≤𝑡≤1, a bug is crawling at a velocity, 𝑣, in meters/hour given by

𝑣=7/(9+𝑡)

Use Δ𝑡=0.2 to estimate the distance that the bug crawls during this hour. Use left- and right-hand Riemann sums to find an overestimate and an underestimate. Then average the two to get a new estimate.

underestimate = 0.7298005 m
overestimate = 0.745356 m
average = 0.7375782 m

Q3. The velocity of a particle moving along the 𝑥-axis is given by 𝑓(𝑡)=6−2𝑡 cm/sec. Use a graph of 𝑓(𝑡) to find the exact change in position of the particle from time 𝑡=0 to 𝑡=4 seconds.

A: change in position = 8 cm

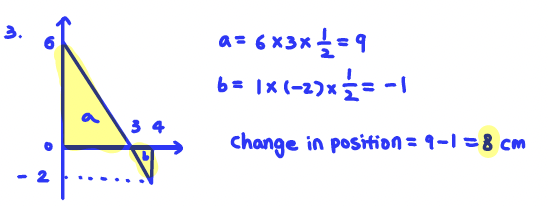
Q4. Two cars start at the same time and travel in the same direction along a straight road. The figure below gives the velocity, 𝑣 (in km/hr), of each car as a function of time (in hr).

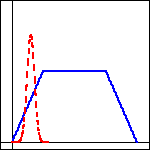
The velocity of car A is given by the solid, blue curve, and the velocity of car B by dashed, red curve.

(a) Which car attains the larger maximum velocity?
A. A
B. B

(b) Which stops first?
A. A
B. B

(c) Which travels farther?
A. A
B. B

 

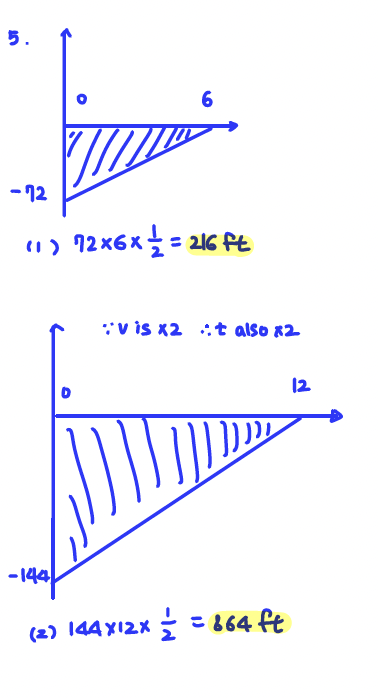
Q5. A car initially going 72 ft/sec brakes at a constant rate (constant negative acceleration), coming to a stop in 6 seconds.

Graph the velocity for 𝑡=0 to 𝑡=6. How far does the car travel before stopping?

A:
distance = 216 ft 

How far does the car travel before stopping if its initial velocity is doubled, but it brakes at the same constant rate?
distance = 864 ft