[Notes & HW Answers] 3.7 Implicit Functions
[Prepwork 3.7]
Q1. Which of the following points satisfies the equation π₯^2−π₯π¦^2=2?
A: (1) (-2^(1/2)/2, (4.5)^(1/4)) ; (2) (-2^(1/2),0)
Q2. (1) Find dy/dx when x^2 - xy^2 =2.
A: (1) dy/dx = (y^2-2x)/-2xy
(2) Find an equation for the tangent line to x^2 - xy^2 = 2 at the point (2,1).
A: (2) y = (3/4)(x-2) + 1
Q3. Find all points satisfying the equation π₯2−π₯π¦2=2x2−xy2=2 where the tangent line is vertical. Give your answers in (π₯,π¦)(x,y) coordinates with commas between points.
A: (2^(1/2), 0), (-2^(1/2), 0)
[HW 3.7]
Q1. Find ππ¦/ππ₯ in terms of π₯ and π¦ if π₯^5+π¦^2= 15^(1/2).
A: dy/dx = -5x^4/ 2y
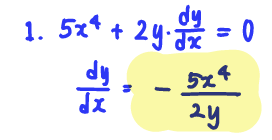
Q2. Find ππ¦/ππ₯ in terms of π₯ and π¦ if 9xy + 8x + y = 7.
A: dy/dx = -(9y + 8) / (9x +1)
Q3. Find ππ¦/ππ₯ in terms of π₯ and π¦ if ax^5 - by^5 = c^5. Assume that a,b and c are constants.
A: dy/dx = ax^4/by^4
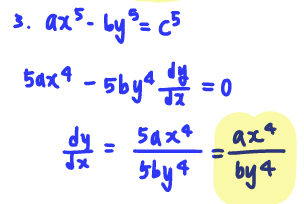
Q4. Find ππ¦/ππ₯ in terms of π₯ and π¦ if xln(y) + y^6 = 8ln(x).
A: dy/dx = - ((ln(y) - (8/x) / (x/y) + 6y^5)
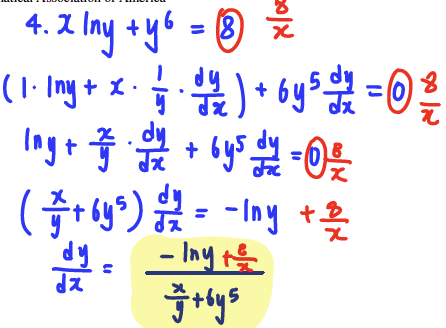
Q5. Find the slope of the tangent to the curve x^3 + 6xy + y^2 = 8 at (1,1). The slope is
A: - 9/8
Q6. Find the slope of the tangent to the curve xy^4 = 1 at (1,-1).
A: dy/dx | _(1,-1) = 1/4
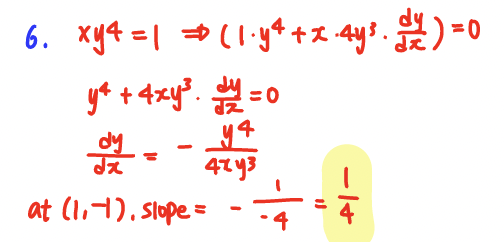
Q7. Find the slope of the tangent to the curve y^2 = x^3 / (xy+6) at (6,3)
A: dy/dx = 81/198
